Fermiho energie je jednou z charakteristik pevných látek. Jak je známo, při vytváření pevné látky se původní energetické hladiny plynných atomů rozštěpí v téměř plynulé pásy. Tento jev je důsledkem Pauliho pravidla, podle kterého žádné dva elektrony v systému nemohou zaujmout stejný stav, vzhledem ke dvěma hodnotám spinu elektronů mohou tedy stejnou energii mít pouze dva elektrony. Pásy, takto vzniklé, mohou se buď překrývat, jako je tomu u kovů, nebo je mezi nimi mezera, takzvaný zakázaný pás. Uvažujeme-li pevnou látku z N atomů, bude mít každý pás právě N podhladin, na něž je možno umístit 2N elektronů. Protože ale máme pouze N elektronů, je možno mít i neobsazené stavy. To, s jakou pravděpodobností bude daná hladina obsazena, závisí na její energii E dle vztahu

  

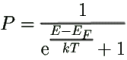
Zde je k Boltzmannova konstanta (přibližně 10^-23 J/K), T absolutní teplota v kelvinech a E_F je právě Fermiho energie. 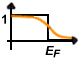Význam této energie je patrný z obrázku. Pro nulovou teplotu je závislost vyznačena černou čárou, podle které je Fermiho energie nejvyšší obsazenou hladinou při T=0 K a všechny pod ní jsou zaplněny s jistotou. Pro vyšší teploty (oranžová čára) se graf pozmění a zde je Fermiho energie interpretovatelná jako hladina s pravděpodobností obsazení 50%.

Ze statistického hlediska má Fermiho energie význam chemického potenciálu. Pro vysvětlení pojmu uvažujme systém velkého počtu elektronů, který je v jistém stavu a má danou energii. Přidáme-li do systému jeden jediný elektron, dá se očekávat, že většina charakteristik se nezmění, vyjma celkové energie. Právě rozdíl energie původní a nynější, tedy energie vnesená částicí, je chemický potenciál, v daném případě Fermiho energie. Protože při velkém počtu elektronů musí totéž platit i pro vyjmutí jednoho elektronu, má Fermiho hladina význam energetické hladiny, z níž elektrony pevnou látku opouštějí. Rozdíl energie vakua a Fermiho energie je tedy výstupní prací kovu.

Uvažujme nyní dva kovy s různými hodnotami E_F, které uvedeme do kontaktu a necháme teplotně ustálit. Protože v tomto případě máme pouze jeden systém a energie, kterou vnese částice by neměla záviset na místě vniku částice, musí se Fermiho energie obou kovů vyrovnat. To je možno tak, že se mezi kovy vytvoří napěťový rozdíl - kontaktní napětí eV=E_F1-E_F2, kde e je náboj elektronu (přibližně 10^-19 C). Vzhledem k tomu, že Fermiho energie závisí na teplotě, závisí na teplotě i kontaktní napětí. Při konstantní teplotě závisí ovšem jen na stýkajících se kovech.