 |
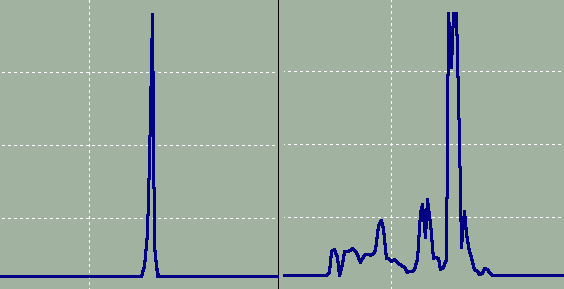
| Změřená rezonanční křivka, vpravo horší nosník. |
Možnost poškození vzorku či kontaminace vzorku z hrotu v dotykové metodě vedla k vývoji metody bezdotykové. Využívá van der Waalsových sil delšího dosahu (na interakci se podílí velké množství atomů, ale charakter interakce je zde dobře znám) a proto se může hrot pohybovat ve vzdálenosti 1–10 nm od povrchu. V uvedené oblasti jsou však síly slabé (celková působící síla bývá řádu 10-12 N), což vyžaduje použití pružného nosníku. Ten ale musí být zároveň tuhý, aby nedošlo k jeho zachycení na povrchu (především v kapkách vody). Proto se častěji používá střídavá technika s nosníkem kmitajícím s frekvencí f, což vede ke zvýšení odstupu signálu od šumu.
Nosník je zde rozkmitáván v okolí své první rezonanční frekvence (zpravidla v rozsahu 100–400 kHz), ovšem s amplitudou vhodně volenou tak, aby nedošlo ke kontaktu se vzorkem. Kvalitní nosník by měl vykazovat pouze jednu ostře ohraničenou rezonanci, v praxi však může frekvenční křivka obsahovat rezonančních píků několik. Je to způsobeno především interakcí s okolním prostředím (vzduchem) a vybuzením mechanických oscilací ve zbytku mikroskopu.
Má-li volný nosník hmotnosti m rezonanční frekvenci ω0 a tuhost k, změní se jeho rezonance v oblasti silového působení v „pružinové aproximaci“ na hodnotu
kde ∂iFj≪k je gradient složky j síly ve směru i. Vstupem do oblasti gradientu sil tedy dojde ke změně rezonance, což se (v případě buzení s konstantní frekvencí) projeví poklesem amplitudy kmitů. Budeme-li pomocí zpětné vazby měnit výšku nosníku tak, aby amplituda kmitů zůstávala konstantní, budeme sledovat křivku konstantního gradientu sil (nikoliv sílu samotnou). Alternativně můžeme zpětnou vazbu vyřadit a sledovat poklesy amplitudy. Jiným využitím může být sledování změn fázového posuvu mezi budicím a detekovaným signálem.
Vertikální rozlišení bezkontaktní metody je dáno jednak schopností detektoru, jednak tepelným pohybem nosníku, jehož amplituda (resp. příspěvek prvního módu) v přítomnosti silového gradientu je přibližně dána vztahem
Dynamický pohyb se zpravidla popisuje v „pružinové“ aproximaci, v níž se nosník uvažuje jako jednorozměrný prvek popsaný efektivní hmotností a tuhostí. Pak můžeme psát pohybovou rovnici
kde Fbud(t) je budicí síla, F(z) síla interakční a z vzdálenost hrotu od vzorku. Koeficient tlumení α je uvažován jako nezávislý na z, což je opodstatněné, pokud předpokládáme elastické výchylky a největší tlumení hydrodynamického původu, které lze v oblastech jednotek nm uvažovat konstantní. Interakční síla je časově nezávislá, protože předpokládáme relaxační časy materiálů značně menší než je perioda oscilací. Můžeme-li ji linearizovat F(z)=-F′(z)z, dostaneme rovnici pružiny s efektivní tuhostí keff=k-F′(z).
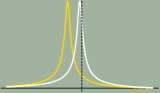 |
| Průběh rezonance volného nosníku (bílá) a posuv křivky vlivem přitažlivé síly (žlutá). |
Systém, popsaný výše uvedenou rovnicí, vykazuje rezonanční charakter a amplituda kmitů je tudíž silně závislá na frekvenci buzení Ω,
kde F0 je amplituda budicí síly. V praxi se používá buzení i detekce s konstantní frekvencí Ω. Vstoupí-li nosník do oblasti s gradientem síly, dojde ke změně rezonanční frekvence a celá křivka se posune. Tím se znatelně změní amplituda, která je detekována, a pokles lze využít buď k mapování sil (topografie), nebo k řízení zpětné vazby, nevýhodou je nejednoznačnost amplitudy. Alternativní metodou je sledování přímo změn rezonanční frekvence, použijeme-li nosník jako frekvenci určující prvek oscilátoru. Předchozí analýza platí v případě, že je rozkmitávána přímo špička nosníku, ale většina AFM přístrojů dosahuje kmitání buzením místa upevnění nosníku (s amplitudou a0). V takovém případě (pokud je nosník schopen danou frekvenci přenést) je nutno analyzovat oscilace ohnutí Δz(t)=z(t)-a0sinΩt, což řešení mírně komplikuje. Vzhled obrazu bude záviset na umístění budicí frekvence vzhledem k rezonanci. Uvažujme, že přibližováním ke vzorku bude narůstat přitažlivá síla, která způsobuje pokles rezonanční frekvence. Bude-li budicí frekvence přesně na rezonanci nebo nad ní, způsobí nárůst síly posun křivky směrem k nižším frekvencím a pokles amplitudy, takže silněji ovlivňující místa (např. vyvýšeniny při konstantní výšce) se budou jevit světlá (je-li obraz inverzí amplitudy). Pokud ale bude budicí frekvence blízko pod rezonancí, nastane nejprve nárůst amplitudy a po přechodu přes rezonanci pokles. Pravděpodobně také dojde k nestabilitě a dotyku se vzorkem.