Předchozí výklad byl pouze ilustrací principu STM. V prostoru vakua dochází sice po přiblížení k vytvoření energetické bariéry a překryvu vlnových funkcí atomů vzorku a hrotu, ale pro stejné materiály je bariéra symetrická a oběma směry teče stejně velký proud a výsledný proud má nulovou střední hodnotu. Teprve po přiložení napětí V dojde k narušení symetrie a nenulovému proudu. Bude-li napětí malé, lze předpokládat příspěvek pouze jediné energetické hladiny a proud bude násobkem pravděpodobnosti tunelování.
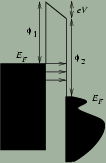 |
| Schéma struktury hrotu a vzorku, V je přiložené napětí, φ1,2 jsou výstupní práce. |
Uvedený vztah pro pravděpodobnost T platí pro průchod částice, která je na obou stranách bariéry volná, což rozhodně nepopisuje elektron v hrotu či vzorku. Z toho plyne také problém nulového kontrastu na rovinném povrchu, což neodpovídá experimentům. Uvedené vztahy totiž nyní závisí na Fermiho energii, která je v celém kovu stejná (v rovnovážném stavu, což není přesně náš případ, protože systémem teče proud), ale proud je rovněž ovlivňován překryvem vlnových funkcí, který se může měnit od atomu k atomu. Dílčím zobecněním je pozměnění celkové pravděpodobnosti tunelování P. Ta totiž závisí nejen na pravděpodobnosti tunelování skrze bariéry, ale také na obsazení příslušných energetických hladin na obou stranách (elektron tuneluje bez ztráty energie, a to jen tehdy, je-li na jedné straně hladina obsazena a na druhé je prázdno). Je zřejmé, že tímto způsobem pravděpodobnost závisí na hustotě energetických stavů, tedy dostane-li se na úroveň Fermiho energie hrotu maximum v hustotě stavů vzorku (změnou velikosti přiloženého napětí), dojde k nárůstu tunelového proudu. Příspěvek různých stavů však není stejný, protože vyšší stavy překonávají nižší bariéru a tunelují tedy s větší pravděpodobností.
Uvažujme tok elektronů, který dopadá ve směru osy z kolmo na bariéru a protuneluje se skrze ní. Počet takových elektronů je Nt=1/m∫0EMn(vz)T(Ez)dEz, kde EM je maximální energie, Ez složka energie v ose z a n(vz)dvz je hustota elektronů s vz∈⟨vz,vz+dvz⟩. Budeme-li předpokládat, že elektrony mají Fermiho distribuci (odpovídá modelu volných elektronů) a zajímat se pouze o závislost v ose z, dostaneme n(vz)=(m3)/(4π3ℏ3)∫-∞∞∫-∞∞f(E)dvxdvy. Dosazením do vztahu pro počet elektronů, vyjádřením analogického počtu pro opačně tunelující elektrony, vynásobením nábojem elektronu a vzájemným odečtením pak dostaneme vzorec pro výslednou hustotu proudu
Z této rovnice plyne pro pravoúhlou bariéru a malé napětí ohmické chování tunelovacího přechodu. Pro větší napětí už se projevují nelinearity (∼V2), které dále zvyšuje efekt zrcadlového náboje.