V technických aplikacích jsou často žádoucí metody, které umožňují vyšetřovat i podpovrchové struktury, což žádná z dosavadních metod neumožňovala. Například polovodičová rozhraní začnou vykazovat zajímavé chování až po svém vytvoření, když již nejsou na povrchu a k vyšetřování je možno použít jen I–V charakteristiky. Ale v případě speciálního tvaru vzorku je možné využít STM hrot k injekci elektronů do podpovrchových vrstev a provádět spektroskopii – metoda BEEM. Podmínkou je vzorek ve tvaru dvou vrstev (vnější – báze – musí být vodivá, zpravidla kovová, vnitřní – kolektor – bývá polovodič) s vyšetřovanou potenciálovou bariérou VB, přičemž svrchní vrstva musí být natolik tenká, aby přes ni injektované elektrony procházely bez znatelné absorpce. Tuto podmínku splňují například Schottkyho diody.
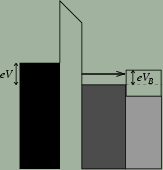 |
| Schéma energetických pásů v BEEM po přiložení napětí V, zleva doprava je hrot, vakuum, báze a kolektor. Přerušovaná čára odpovídá Fermiho energii vzorku. |
Základem tedy je trojelektrodové uspořádání, dvě elektrody tvoří vzorek, třetí hrot. Polovodič je typu n, aby byly elektrony od přechodu s hrotem odsávány a nevracely se. Po přiložení tunelovacího napětí mohou elektrony tunelovat skrz vakuum do polovodičové struktury, kde mají přebytečnou energii eV, kterou však neztrácejí okamžitě a přemísťují se v objemu vzorku s malou interakcí, charakterizovanou střední volnou dráhou. Je-li velikost prostřední vrstvy menší než volná dráha (cca. 10 nm), mohly by také projít přes přechod bez ztráty energie srážkou, pokud budou splněny zákony zachování celkové energie a hybnosti podél rozhraní. Pokud však je V<VB, nemají na přechod dostatečnou energii a proud IC měřený v obvodu kolektoru je malý. Jakmile však zvýšíme V nad VB, tekoucí proud prudce vzroste. Prostorové variace v IC lze použít k zobrazování, závislost IC–V pak ke stanovení elektronických vlastností přechodu.
Jednoduchý model teorie BEEM uvažuje tři následné procesy — vakuové tunelování, transport elektronů bází a transport přes rozhraní, přičemž nezahrnuje dynamické efekty (např. kvantově–mechanický odraz na rozhraní). Nejjednodušší model rozhraní je dokonale hladký, pravoúhlý potenciálový schod, zachovává se rovnoběžná složka vlnového vektoru kt, ale mění se kolmá kx, protože se mění kinetická energie. Není-li dopad kolmý, vyžaduje tato změna změnu směru částice, která může být dokonce tak velká, že pro dopadový úhel větší než kritický Θk dojde k odrazu. Existence kritického úhlu zajišťuje vysoké prostorové rozlišení metody, velikost úhlu je sinΘk=(E-E0)/E, kde E je celková energie a E0=EF+eVB (jiná interpretace je nutnost Ex=(ℏ2kx2)/(2me)>E0). Pro reálná rozhraní je situace bohužel složitější, protože nelze provést rozdělení na kx a kt. Kritický úhel pak začíná záviset na poměru efektivních hmotností v kolmém a rovnoběžném směru v kovu i polovodiči. Např. pro Au na Si má kužel vrcholový úhel 6°. Získané rozlišení je přibližně 1 nm pro bázi tlustou 10 nm.
Injekce elektronů tunelováním je charakterizována především pravděpodobností tunelování D(Ex)≈e-2∫kxdx (přesněji by měla záviset i na celkové energii) a proud je dán vztahem
kde S je efektivní plocha, f(E) Fermi–Diracova statistika a vx=(ℏkx)/m. Uvažuje-li se stejný kov pro bázi i hrot, nulová teplota (vhodné stavy tedy leží ve Fermiho kouli mezi E=EF-eV a E=EF) a omezení kritickým úhlem (Et≤(mt)/(m-mt)[Ex-EF+e(V-VB)] pro mt<m, Ex≥EF-e(V-VB)), vychází pro výsledný kolektorový proud
kde C je konstanta a R je míra zeslabení rozptylem v bázi (uvažuje se nezávislá na E). Je-li eVB≫kBT, lze zanedbat f(E+eV) a integrace přes Et je analyticky vyjádřitelná, pro nulovou teplotu je analytická i druhá integrace.
Z technického hlediska je metoda náročnější, protože měřené proudy jsou řádově menší, je zapotřebí čistý povrch (vakuum) a je nutno ovládat tři napětí.