V předchozím textu bylo na zobrazení AFM nazíráno jako na konvoluci hrotu a vzorku. Někdy je správnější uvažovat obraz jako nelineární, morfologickou operaci dilatace povrchu vzorku strukturním elementem, jímž je hrot. Pro obraz tedy platí z=s⊕t, kde s popisuje povrch, t hrot a z získaný obraz, ⊕ je označení dilatace. Známe-li tvar hrotu (který můžeme přibližně získat ze zobrazení známého povrchu), můžeme kvalitu obrazu vylepšit „inverzní“ morfologickou operací, erozí, tedy r=z⊖t, kde r je rekonstruovaný povrch a ⊖ je eroze. Problémem zůstává pouze to, že dilataci provádíme skutečným hrotem, erozi jeho odhadem. Rekonstruovaný obraz vykazuje tři různé oblasti: v první platí r=z=s a není zde žádné zkreslení, ve druhé platí r=s, z≠s a rekonstruovaný obraz je shodný se skutečným, ve třetí oblasti už průběhy shodné nejsou, ale r je lepší než z.
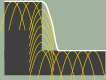 |
| Modelování obrazu obálkou. |
Alternativně lze rekonstrukci obrazu provádět pomocí Legendreovy transformace, která v oblastech bez vícenásobného doteku hrotu dává pro ideální obraz stejné výsledky jako eroze. Výsledky se však mohou lišit pro zašuměný obraz. (V oblastech násobného doteku morfologie obtiskuje tvar hrotu, Legendreova transformace ponechá prázdné místo). Propracováním metody v jednom rozměru dojdeme ke vztahu pro stupeň zkreslení
(d(x-x′))/(dx′)=((d2z)/(dx′2))/((d2t)/(d(x-x′)2)),
ze kterého plyne očekávaný poznatek, že obraz je méně zkreslen, je-li křivost hrotu větší než křivost vzorku (souřadnice x a x′ odpovídají funkcím skutečného a zdánlivého povrchu).
Metoda rekonstrukce pomocí obálky je třetím přístupem, který opět dává shodné výsledky pro informační oblasti. Je založena na jednoduchém principu – hrot (v přímé poloze) umístíme do každého bodu obrazu a rekonstruovaným obrazem bude obálka těchto hrotů. Tento princip odpovídá vzniku obrazu klouzáním hrotu po vzorku, obálka zaručí získání nejnižší možné polohy hrotu (není fyzikálně možné, aby byť jen jeden z rekonstruujících hrotů byl v prostoru vyplněném vzorkem). Matematicky je rekonstruovaný obraz dán vztahem
(funkce obrazu z a hrotu t musí mít dolní mez). I v této metodě existují oblasti, v nichž není rekonstrukce možná – obtiskne se hrot.
Metoda obálek se dá rovněž použít ke konstrukci obrazů z modelů: Každý bod skutečného povrchu s se považuje za tenkou špičku s patřičnou výškou, na niž se posadí invertovaný a převrácený hrot (-t(-x,-y)), obraz je pak dán obálkou hrotů
z(x,y)=max{s(x′,y′)-t(x′-x,y′-y) ∀(x′,y′)∈ℜ} ∀(x,y)∈ℜ.
Zajímavý jetaké reciproční teorém, který říká, že zobrazením spodní strany naměřeného obrazu (v 3D vyjádření) obráceným hrotem získáme rekonstruovaný povrch.