Elektronika a zpětná vazba

Elektronika, kterou musí být SPM přístroj vybaven, zahrnuje několik částí.

• Napěťové zdroje pro vlastní elektroniku.
• Generátory pro řízení piezokeramiky, které vytváří pomalý a rychlý skenovací signál. Pomalý signál může být pilovitý, ale u rychlého je to nevhodné kvůli excitacím vyšších harmonických složek.
• Vysokonapěťové zesilovače napětí pro piezokeramiku.
• Elektronické zesilovače detekovaných signálů (v STM musí mít velký dynamický rozsah) a obvody pro jejich okamžité zpracování.
• Obvod zpětné vazby
• Doplňující obvody dle typu metody (zdroj pro tunelový přechod v STM, laser v AFM, zádržné obvody pro STS, …).
• Obvody pro komunikaci s počítačem, využívající zpravidla standardní rozhraní a PC karty s DSP. Pro přenos dat a řízení je nutno používat A/D a D/A převodníky. Před digitalizací musí být signál nejprve upravován odstraněním nízkofrekvenční složky, způsobené velkým náklonem vzorku, aby nedošlo k překročení rozsahu A/D převodníku.
• Počítač pro uchovávání, zpracování a zobrazování měření.

Obvod zpětné vazby

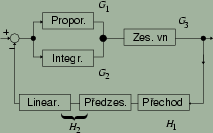
K regulaci se zpravidla používá PID regulátor, i když derivační složka je téměř vždy nulová a proporcionální má jen omezený vliv. Nejdůležitější je tedy integrační, která zásadním způsobem ovlivňuje získaný obraz (především zákmity). Požaduje se velmi krátká odezva (omezuje rychlost skenování) a takový zisk, aby byl malý při vlastních frekvencích systému a vysoký pro nulovou frekvenci (kvalitní nastavení polohy). Zpětná vazba může být provedena i digitálně, vnáší se ovšem chyby kvantování a konečné rychlosti vzorkování, stavba je náročnější, ale je snazší případná změna režimu práce (pouze přeprogramování). Části systému se při modelování uvažují lineární a hledá se celková přenosová funkce mikroskopu.

V praxi jsou dány parametry zesilovačů a přechodu a je možno manipulovat pouze s parametry PI regulátoru tak, aby se minimalizoval chybový signál za podmínek dosažení stabilního systému (chybový signál nesmí růst s časem nade všechny meze), malé ustálené chyby a rychlé přechodové odezvy. Pro dosažení malé chyby je nutné velké zesílení, ale to snižuje stabilitu. Proto je nutno mít i integrační člen, popř. zařadit za proporcionální dolní propust. Pro rychlou odezvu je nutno použít derivační člen, který „předpovídá“ budoucí hodnoty a umožňuje rychlou reakci, ovšem za cenu snížení stability a zvětšení vysokofrekvenčního šumu (derivace → násobení ω, nutnost filtru). Použití derivačního členu navíc stěžuje analýzu, protože tíhne k řízení velkými signály, které mohou být mimo platnost lineární aproximace.

Zpětná vazba v STM

Pro případ tunelovacího mikroskopu můžeme použít následující charakteristiky:
G₁(s)=(K_P)/(sτ_P+1), G₂(s)=(K_I)/((sτ_P+1)s), G₃(s)=(K_Z)/(sτ_Z+1),
H₁(s)=(ω²K_T)/(s²+ω_ns/Q+ω_n²), H₂(s)=(K_L)/(sτ_L+1),
kde K_i a τ_i jsou příslušné konstanty obvodu, ω_n a Q charakterizují tunelový přechod a určí se experimentálně. Celkový přenos je pak dán
T=([G₁+G₂]G₃)/(1+[G₁+G₂]G₃H₁H₂).
Jediná část, která není lineární, je vlastní tunelový přechod, proto bývá jeho výstup linearizován v logaritmickém zesilovači.